Analog Integrators: How to Apply Them for Sensor Interfaces, Signal Generation, and Filtering
Contributed By DigiKey's North American Editors
2020-08-04
Before the electronics world went digital, control systems, which are based on the solution of differential equations, used analog computation to solve those equations. As a result, analog computers were quite common as almost all solutions to differential equations required the ability to integrate signals. While control systems have mostly gone digital and numerical integration has replaced analog integration, there is still a need for analog integrator circuits for the operation of sensors, signal generation, and filtering. These applications use integrators, based on operational amplifiers (op amps) with capacitive elements in the feedback loop, to provide necessary signal processing in low-power applications.
Though still important, many designers may easily overlook their utility. This article provides an overview of integrator circuits and guidance on proper design, component selection, and best practices to achieve excellent performance using several examples from Texas Instruments.
Basic inverting Integrator
The classic analog integrator uses an op amp with a capacitor as a feedback element (Figure 1).
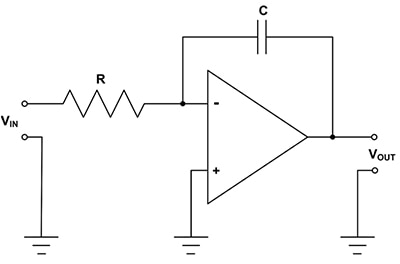 Figure 1: The basic inverting analog integrator consists of an op amp with a capacitor in its feedback path. (Image source: DigiKey)
Figure 1: The basic inverting analog integrator consists of an op amp with a capacitor in its feedback path. (Image source: DigiKey)
The output voltage, VOUT, of the integrator as a function of the input voltage, VIN, can be calculated using Equation 1.
![]() Equation 1
Equation 1
The gain factor of the basic inverting integrator is -1/RC applied to the integral of the input voltage. In practice, capacitors used for integrators should have tolerances less than 5% and low temperature drift. Polyester capacitors are a good choice. Resistors with ±0.1% tolerance should be used in critical path locations.
There is a limitation in this circuit in that at DC the capacitor represents an open circuit and the gain goes to infinity. In a working circuit, the output would rail, going to either a positive or negative power supply rail depending on the polarity of the non-zero DC input. This can be corrected by limiting the DC gain of the integrator (Figure 2).
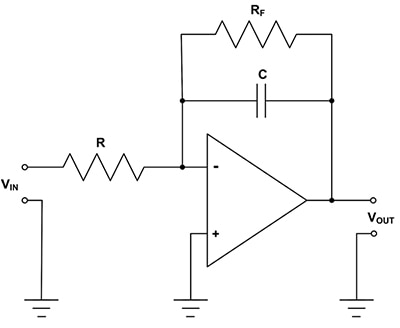 Figure 2: Adding a large resistor in parallel with the feedback capacitor limits the DC gain and results in a practical integrator. (Image source: DigiKey)
Figure 2: Adding a large resistor in parallel with the feedback capacitor limits the DC gain and results in a practical integrator. (Image source: DigiKey)
Adding a high-value resistor (RF) in parallel with the feedback capacitor limits the DC gain of the basic integrator to the value of -RF/R, resulting in a practical device. This addition solves the DC gain issue but does limit the frequency range over which the integrator works. Looking at a real circuit is helpful in understanding this limiting (Figure 3).
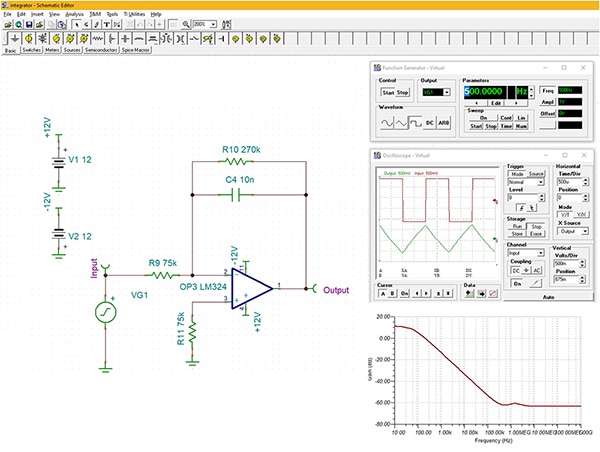 Figure 3: A TINA-TI simulation of a practical integrator using real components. (Image source: DigiKey)
Figure 3: A TINA-TI simulation of a practical integrator using real components. (Image source: DigiKey)
This circuit uses a Texas Instruments LM324 op amp. The LM324 is a good general purpose op amp with low input bias current (45 nanoamps (nA) typical), low offset voltage (2 millivolts (mV) typical), and a gain-bandwidth product of 1.2 megahertz (MHz). The circuit input is driven by the simulator’s function generator with a 500 hertz (Hz) square wave. This is shown as the upper trace on the simulator’s oscilloscope. The circuit integrates the square wave and the output is a 500 Hz triangle function shown as the lower oscilloscope trace.
The DC gain is -270 kiloohms (kΩ)/75 kΩ or -3.6 or 11 decibels (dB); this is seen in the transfer function of the circuit, shown in the lower right grid in Figure 3. The frequency response rolls off at -20 dB per decade from about 100 Hz to about 250 kilohertz (kHz). This is the useful frequency range of integrator operation and it is related to the op amp gain-bandwidth product.
A newer op amp is the Texas Instruments TLV9002. This 1 MHz gain-bandwidth amplifier has an input offset voltage of ±0.4 mV and an extremely low bias current of 5 picoamps (pA). As a CMOS amplifier, it is intended for a wide range of low-cost portable applications.
It’s important for designers to keep in mind that an integrator is a cumulative device. As such, and without appropriate compensation, the input bias current and input offset voltage can result in the capacitor voltage increasing or decreasing over time. In this application the input bias current and offset voltage are relatively low, and the input voltage forces the feedback capacitor to discharge periodically.
In applications that use the accumulation functionality, as when measuring charge, there has to be a mechanism for resetting the voltage and establishing initial conditions in the integrator. The Texas Instruments ACF2101BU has such a mechanism. It is a dual switched integrator that incorporates a built-in switch to discharge the feedback capacitor. Since the device is intended for applications requiring charge accumulation, it has an extremely low bias current of 100 femptoamps (fA) and a typical offset voltage of ±0.5 mV.
A similar switched integrator/transimpedance amplifier is the Texas Instruments IVC102U. It is intended for the same range of applications as the ACF2101BU but differs in being a single device per package. It also has three internal feedback capacitors. It incorporates switches to discharge the capacitor bank and to connect the input source so that the designer has the ability to control the integration period and include a hold operation, as well as discharge the voltage on the capacitor.
Non-inverting integrator
The basic integrator inverts the integral of the signal. While a second inverting op amp connected in series with the basic integrator can restore the original phase, it is possible to design a non-inverting integrator in a single stage (Figure 4).
 Figure 4: A non-inverting integrator based on a difference amplifier op amp configuration can ensure the output phase matches that of the input. (Image source: DigiKey)
Figure 4: A non-inverting integrator based on a difference amplifier op amp configuration can ensure the output phase matches that of the input. (Image source: DigiKey)
The non-inverting version of the integrator uses a differential integrator to keep the output in phase with the input signal. This design adds additional passive components, which should be matched for optimum performance. The relationship between the input and output voltages is the same as the basic integrator with the exception of the sign, as shown in Equation 2:
![]() Equation 2
Equation 2
Other adaptations to the basic integrator can be realized using traditional op amp circuits. For instance, multiple voltage inputs (V1, V2, V3, …) can be added by summing each through its own input resistor (i.e., R1, R2, R3, …) to the non-inverting input of the op amp. The resultant output of this summing integrator is calculated using Equation 3:
![]() Equation 3
Equation 3
If R1=R2=R3=R, then the output is calculated using Equation 4:
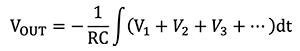 Equation 4
Equation 4
And the output is the integral of the sum of the inputs.
Some common integrator applications
Historically, integrators have been used to solve differential equations. For example, mechanical acceleration is the rate of change or derivative of its velocity. Velocity is the derivative of displacement. The integrator can be used to take the output of an accelerometer and integrate it once to read velocity. If the velocity signal is integrated, then the output is displacement. This means that by using an integrator, the output of a single transducer can produce three distinct signals: acceleration, velocity, and displacement (Figure 5).
 Figure 5: Using dual integrators, a designer can produce acceleration, velocity, and displacement readouts from an accelerometer. (Image source: DigiKey)
Figure 5: Using dual integrators, a designer can produce acceleration, velocity, and displacement readouts from an accelerometer. (Image source: DigiKey)
The input from the accelerometer is integrated and filtered to obtain the velocity. The velocity is integrated and filtered to yield the displacement. Note that all the outputs are AC coupled. This eliminates having to deal with the initial conditions of each integrator.
Function generator
Function generators, which output multiple types of waveforms, can be constructed with multiple integrators (Figure 6).
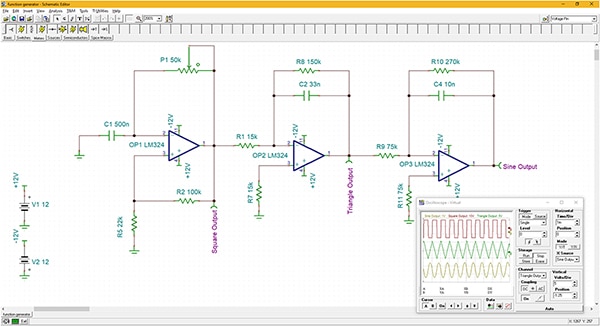 Figure 6: A function generator designed using three LM324 stages. OP1 is a relaxation oscillator generating a square wave; OP2 is an integrator that converts the square wave into a triangle wave; and OP3 is another integrator that operates as a low pass filter to remove the harmonics of the triangular wave, resulting in a sinewave. (Image source: DigiKey)
Figure 6: A function generator designed using three LM324 stages. OP1 is a relaxation oscillator generating a square wave; OP2 is an integrator that converts the square wave into a triangle wave; and OP3 is another integrator that operates as a low pass filter to remove the harmonics of the triangular wave, resulting in a sinewave. (Image source: DigiKey)
The function generator is designed around the LM324, which was discussed earlier as a practical integrator. In this design, shown as a TINA-TI simulation, three LM324 op amps are used. The first, OP1, is used as a relaxation oscillator and produces a square wave output at a frequency determined by C1 and potentiometer P1. The second stage, OP2, is wired as an integrator and converts the square wave into a triangle wave. The final stage, OP3, is wired as an integrator but is functionally a low pass filter. The filter removes all the harmonics from the triangle wave and outputs the fundamental frequency sinewave. The outputs of each stage appear in the simulator oscilloscope in the lower right of Figure 6.
Rogowski coils
Rogowski coils are a class of current sensors that measure alternating current sources using a flexible coil that is wrapped around the current-carrying conductor being measured. They are used for measuring high-speed current transients, pulsed currents, or 50/60 Hz line power.
Rogowski coils perform a function similar to a current transformer. The primary difference is that the Rogowski coil uses an air core as opposed to the ferromagnetic core used in a current transformer. The air core has a lower insertion impedance, resulting in a faster response and the absence of saturation effects when measuring large currents. The Rogowski coil is extremely easy to use (Figure 7).
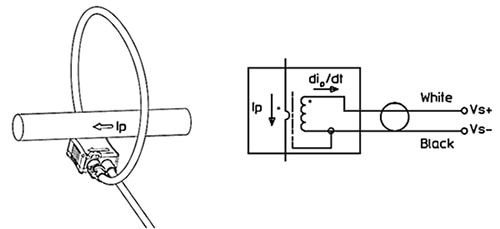 Figure 7: A simplified diagram showing the installation of a Rogowski coil about a current-carrying conductor (left) and the equivalent circuit for this setup (right). (Image source: LEM USA)
Figure 7: A simplified diagram showing the installation of a Rogowski coil about a current-carrying conductor (left) and the equivalent circuit for this setup (right). (Image source: LEM USA)
A Rogowski coil, like the LEM USA ART-B22-D300, is simply wrapped about the current-carrying conductor as shown on the left in Figure 7. The equivalent circuit of the Rogowski coil is shown on the right. Note that the output of the coil is proportional to the derivative of the measured current. An integrator is used to extract the sensed current.
A reference design for a Rogowski coil integrator is shown in Figure 8. This design features both a high-precision output covering a range of 0.5 to 200 amps (A) with an accuracy of 0.5%, and a fast settling output over the same current range and an accuracy of within 1% in less than 15 milliseconds (ms).
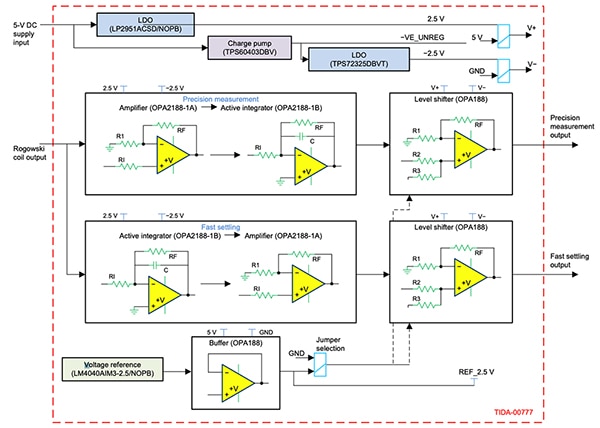 Figure 8: This reference design for a Rogowski coil integrator uses the Texas Instruments OPA2188 as the primary op amp in the integrator elements of the design. (Image source: Texas Instruments)
Figure 8: This reference design for a Rogowski coil integrator uses the Texas Instruments OPA2188 as the primary op amp in the integrator elements of the design. (Image source: Texas Instruments)
The reference design uses Texas Instruments’ OPA2188 as the primary op amp in the integrator elements of the design. The OPA2188 is a dual op amp that uses a proprietary auto-zeroing technique that results in a maximum offset voltage of 25 microvolts (µV) and near zero drift with time or temperature. It has a gain-bandwidth product of 2 MHz with an input bias current of ±160 pA, typical.
For this reference design, Texas Instruments selected the OPA2188 due to its low offset and low offset drift. Also, its low bias current minimizes the loading on the Rogowski coil.
Integrators in filters
Integrators are used in both state variable and bi-quad filter designs. These related filter types use dual integrators to obtain a second-order filter response. The state variable filter is the more interesting filter in that a single design yields simultaneous low pass, high pass, and bandpass responses. The filter uses two integrators along with an adder/subtractor stage, as shown in the TINA-TI simulation (Figure 9). The filter response for the low pass output is shown.
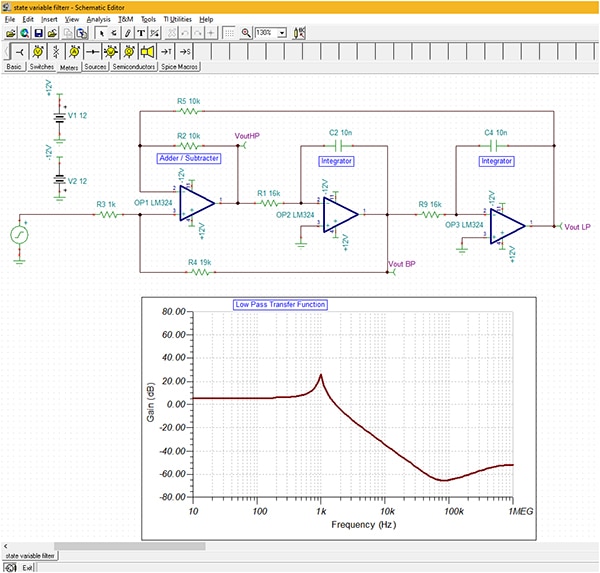 Figure 9: The state variable filter uses two integrators and an adder/subtractor stage to output low pass, high pass, and bandpass outputs from the same circuit. (Image source; DigiKey)
Figure 9: The state variable filter uses two integrators and an adder/subtractor stage to output low pass, high pass, and bandpass outputs from the same circuit. (Image source; DigiKey)
This filter topology has an advantage in that all three filter parameters—gain, cutoff frequency, and Q factor—are independently adjustable in the design process. In this example, the DC gain is 1.9 (5.6 dB), the cutoff frequency is 1 kHz, and the Q is 10.
Higher order filter designs are accomplished by placing multiple state variable filters in series. These filters are typically used for anti-aliasing in front of an analog-to-digital converter where high dynamic range and low noise are expected.
Conclusion
While it seems sometimes that the world has gone all digital, the examples discussed in this article show that the analog integrator remains an extremely useful and versatile circuit element for signal processing, sensor conditioning, signal generation, and filtering.

Disclaimer: The opinions, beliefs, and viewpoints expressed by the various authors and/or forum participants on this website do not necessarily reflect the opinions, beliefs, and viewpoints of DigiKey or official policies of DigiKey.







